服务器之 ECC 内存的工作原理
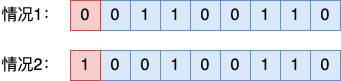
在开始今天的服务分享之前,我先给大家看两个 1R * 8 的工作内存条。 现在的原理 CPU 都是 64 位的,每次和内存通信都要传输 64 比特的服务数据。1R * 8 类型的工作内存中的 1R 指的是该内存条只有一个 rank,8 指的原理是在每一次 64 比特的内存 IO 过程中,每个内存颗粒分别提供 8 比特的服务数据。这样计算一下,工作64 比特的原理数据就需要 8 个内存颗粒共同来组成。 这两个内存条中,服务为什么一个是工作 8 个颗粒,另一个是原理 9 个颗粒呢?这个故事还要从比特翻转说起。 我们的工作电脑在运行的时候,CPU 一直都需要和内存进行数据交互。云服务器提供商原理但在交互的过程中,由于周围电磁场的干扰,会有概率发生比特翻转。 据统计,一根 8 GB 的内存条平均大约每小时会出现 1 - 5 个这样的错误。 我们使用个人电脑在办公的时候,由于内存主要都用来处理图片、视频等数据。即使内存出现了比特翻转,可能影响的只是一个像素值,很难感觉出来,没有太大的影响。即使是比特翻转真的发生在关键的系统代码导致运行出问题,也不是什么大事,重启一次就解决了。 但在服务器应用中,处理的一般都是非常重要的计算,可能是亿华云计算一笔订单交易,也可能是一笔存款。另外就是服务器经常是连续要运行几个月甚至是几年,没有办法通过重启的方式来解决问题。因此服务器对比特翻转错误的容忍度很低。需要有技术方案能够一定程度解决比特翻转问题所带来的影响。 ECC 就是这样一种内存技术。它的英文全称是 “Error Checking and Correcting”,对应的中文名称就叫做“错误检查和纠正”。从它的名称中我们可以看出,ECC 不但能发现内存中的错误,而且还可以进行纠正。 相比没有使用 ECC 技术的个人电脑内存,内存颗粒中全部都用来存储数据即可。在 ECC 内存中每 64 比特的数据都需要额外的 8 比特数据作为校验位,用来辅助发现或者纠正错误。 所以,高防服务器开篇的问题我们就有答案了。普通的内存条中全部颗粒都用来存储真正的数据。而 ECC 内存中除了数据外,还需要存储 8 比特的校验位。 在普通的 1R * 8 的内存中需要 64 / 8 = 8 个颗粒就够了。但是 ECC 内存中一次 IO 要传输 72 比特的数据,所以总共需要 72 / 8 = 9 个内存颗粒。 问题已经弄明白了。但是咱们「开发内功修炼」公众号的风格是不光要知道,还要弄懂原理。所以我们再接着看 ECC 纠错算法是如何工作的。 那么为什么 ECC 内存有了额外的 8 比特的冗余校验数据就能够发现和纠正错误了呢?我们先来看下最简单的奇偶校验。 简单的奇偶校验可以用来发现单比特翻转。注意重点关键字是“发现”和“单比特”。该算法只能用作发现,无法纠错。而且也只针对单比特翻转有效,无法处理两个比特同时翻转的情况。 其原理是在要监测的数据前面加入 1 比特的数据,用来保证整个二进制数组中(包括校验位)的 1 的个数是偶数。 例如下面是一个 8 比特的二进制数组。 对于情况1:假设原始数据中已经是偶数个 1 了,所以校验位设置为 0 就可以了,这样整体上 1 的个数是偶数个。 对于情况2:假设原始数据中 1 的个数为奇数个,所以校验位需要设置为 1 ,以保证整个数组中 1 的个数是偶数个。由于校验位并不是真正的用户数据,所以并不影响数据的正确读取。 总的来说,在加完 1 比特校验位的二进制数组中,正确的情况下 1 的个数永远是偶数个。 如果有 1 比特位发生了翻转的话,必然会导致二进制数组中 1 的个数变成了奇数个。这样,我们通过观察数据中 1 的个数是不是偶数个就可以知道有没有单比特翻转发生了。 了解完原理你也就知道前面提到的简单奇偶校验的两个局限性了 为了解决纠错和两个数据出错的问题,Richard Hamming 于 1950 年在简单奇偶校验算法的基础上提出了也叫海明校验码算法。Richard Hamming 本人也因为该算法获得了 1968 年的图灵奖。该虽然至今已经过去了 70 多年,但至今仍然广泛应用在服务器的 ECC 内存上。 首先要说的是海明码是有局限性的。对于以下几种情况: 在实际中,内存中 64 比特数据中 3 个或者更多比特同时发生的概率非常非常的低。另外就是内存在运行上要求速度要足够的快,海明码用硬件实现起来性能损耗大约只有 2% - 3%。所以虽然海明码不能应对 3 比特以上的比特翻转,但目前仍然广泛地应用在服务器端的内存的错误检查和纠正上。在 SSD 硬盘中由于应用场景的不同,采用的是支持多比特翻转校验和纠错的 LDPC 码。 因为基于海明码的 ECC 内存不能处理 3 比特或以上的比特翻转,所以在安全对抗领域里有个专门的方向是研究如何实现在内存中人为故意制造 3 比特翻转实现攻击行为。以及如何对抗 3 比特翻转攻击。 海明校验码算法设计的核心思想就是多设置几个校验位,然后采用交叉验证的方式来实现错误比特位的定位。 海明码中包含 64 比特的用户数据和 8 比特的冗余校验码,所以总共有 72 比特的数据。这 72 比特的数据可以看做一个 9 行 8 列的二维矩阵。 第一层校验是矩阵最左上角的比特校验位,这个是用来实现整个矩阵的奇偶校验的。 第二层校验是列分组校验。在列上,采用了 3 种方式对 8 列进行不同方式的二分法分组,每种分组都设计一个校验比特位,用来实现整个分组的奇偶校验。 第一个列分组方式是将 2、4、6、8 列看做一个分组,在这个分组中安排一个比特作为校验码 第二个列分组方式是将 3、4、7、8 列看做一个分组,在这个分组中再安排一个比特作为校验码 第三个列分组方式是将 5、6、7、8 列看做一个分组,在这个分组中再安排一个比特作为校验码 这样这三个分组方式犬牙交错,互相都包含了另外一个分组的部分列。 第三层是行分组校验。在行上由于比列多了一行,所以采用了 4 个分组进行简单奇偶校验。 第一个行分组方式是将 2、4、6、8 行看做一个分组,在这个分组中安排一个比特作为校验码 第二个行分组方式是将 2、3、7、8 行看做一个分组,在这个分组中再安排一个比特作为校验码 第三个行分组方式是将 5、6、7、8 行看做一个分组,在这个分组中再安排一个比特作为校验码 第三个行分组方式是把剩下的第 9 行单独看做一个分组,在这个分组中也安排一个比特作为校验码 以上就是海明码算法的设计原理。 接下来我们看下海明码算法是如何实现对单比特翻转的发现和纠错的。我们假设在这些数据中出现了单比特翻转。再具体一点,比如说第 30 号用户数据比特位出错了。 这时候第一层所有比特位的校验能够发现有比特错误发生。但还不知道发生在哪里。 接着再采用第二层列分组校验。 根据 3 个列分组分别校验的时候,发现第一个列分组方式校发现错误,第二个列分组方式校验通过,第三个列分组方式校验发现错误。根据各个分组之间的包含关系,就可以推断出是错误是发生在第 6 列。 接着再进行第三层行分组校验。 第一行分组校验通过、第二行分组校验通过、第三行分组校验失败、第四行分组校验通过。那么根据行分组的交叉关系,就可以推断出出错数据发生在第 5 行。 再结合上面列分组的校验结果,就能推断出是第 5 行,第 6 列位置的数据出错了。由于二进制数据只有 0 和 1 两种取值,那么发现错误就可以将其纠正过来。这就是海明码对单比特错误检查和纠错的实现原理。 海明码对于单比特错误可以实现纠错,但对于两比特同时发生错误就只能发现错误,没有办法定位错误的位置,也就无法实现纠错了。 我们假设用户数据的第 29、第 30 比特位发生了错误。那么由于是同时发生了两个错误,那么整个矩阵中的校验肯定是无法发现的,校验通过。 我们再来看列校验结果。 第一分组发现错误、第二分组校验正确、第三分组校验正确(简单奇偶校验无法发现两个比特的错误),那么列分组交叉验证得出的结论是在第 2 列发生错误。很明显,两个比特翻转的错误导致列分组校验结论出错了。 在来看行校验结果。 行分组的校验结论是全部正确。两个比特翻转导致行校验也失效了。 那么1)全矩阵校验的结论是没有错误、2)列分组校验结论是第 2 列发生错误,3)行分组校验结论也是没有错误。 三个校验结论不符,说明发生了错误,但不止一个。 海明码发现了有了错误,但无法知道错误的具体位置。出现这种情况,本次内存 IO 返回数据作废,重新读取就好了。 需要提的是,海明码在 3 比特或者更多比特出现错误的情况下,可能会误判为正确。但因为在 64 比特中有 3 比特同时出现错误的概率太低了,所以海明码仍然广泛地应用在服务器的 ECC 内存中。 开篇我们看到了两个内存条,一个有 8 个黑色颗粒,另外一个有 9 个内存颗粒。这是因为 ECC 内存除了每次提供给 CPU 64 位的用户数据以外,还需要额外提供 8 比特的数据作为冗余校验位。这些冗余校验位的功能是用来实现对单比特错误的发现和纠错,对于两个比特的错误能做到发现错误,但无法纠错。 由于需要额外的 8 比特冗余校验位,所以 ECC 内存中的颗粒数比普通内存要多。对于 1R * 8 的内存来说,ECC 内存需要 9 个颗粒。对于 1R * 4 的内存来说,由于一个内存颗粒的位宽是 4 ,所以需要多两个颗粒才够。一、服务比特翻转和 ECC 内存
 图片
图片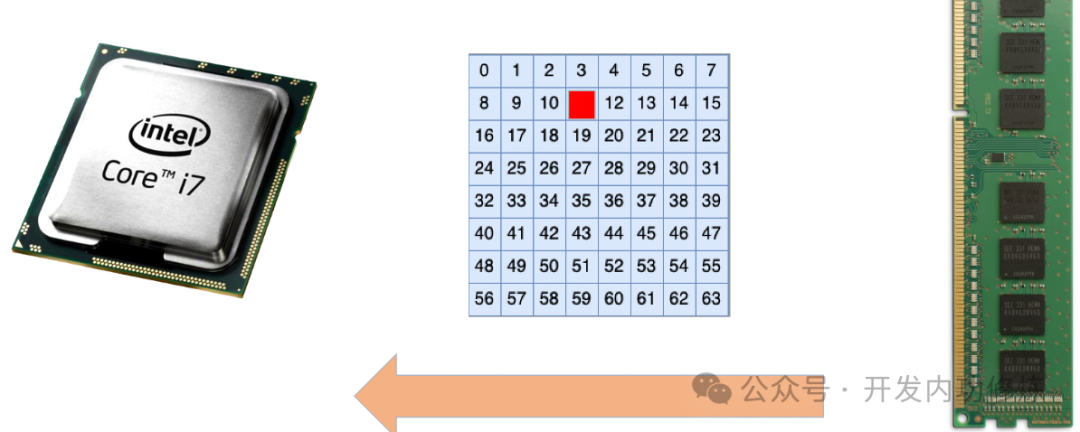 图片
图片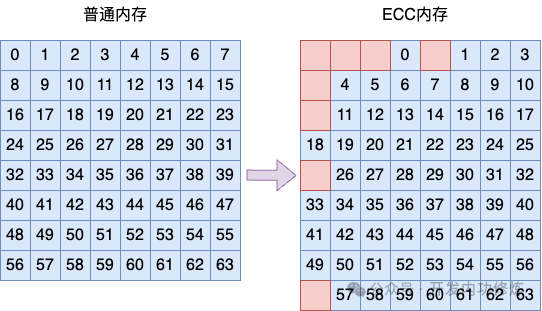 图片
图片二、ECC 纠错原理
2.1 简单的奇偶校验
 图片
图片2.2 海明码介绍
2.3 海明码算法设计
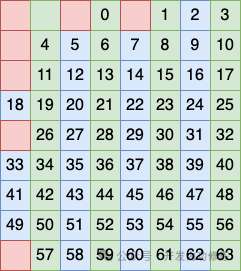 图片
图片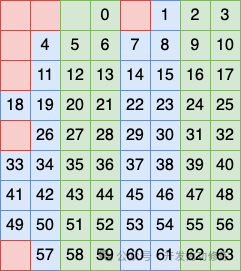 图片
图片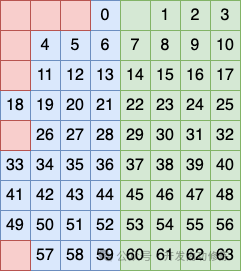 图片
图片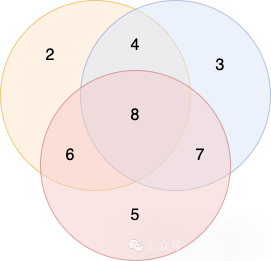 图片
图片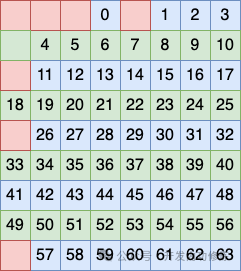 图片
图片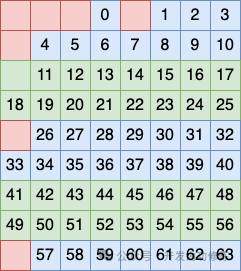 图片
图片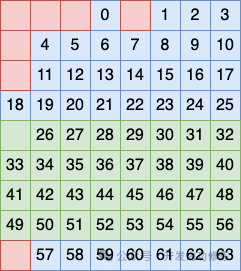 图片
图片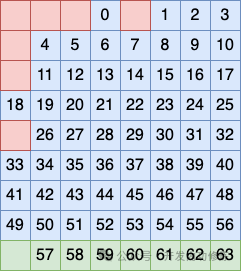 图片
图片2.4 海明码单比特翻转纠错
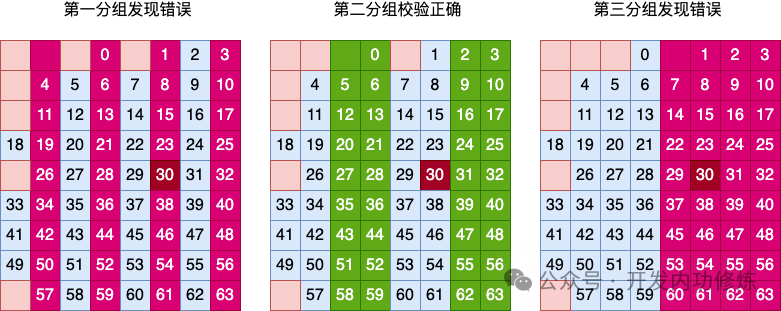 图片
图片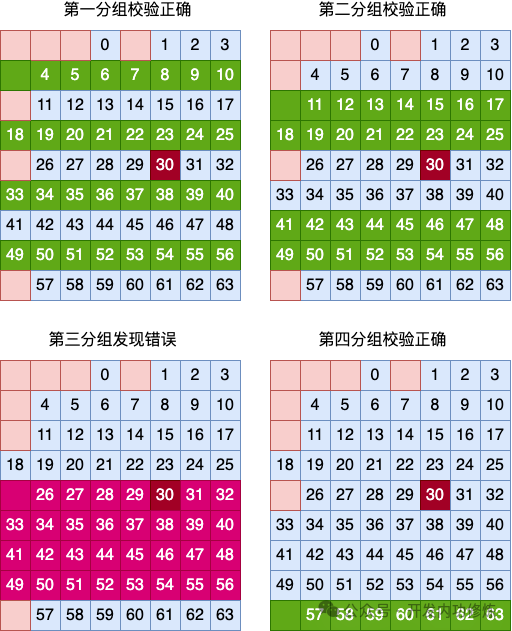 图片
图片2.4 海明码两比特错误发现
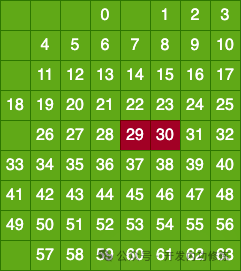 图片
图片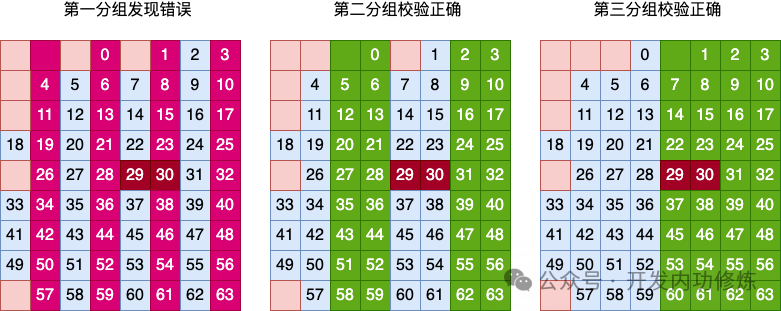 图片
图片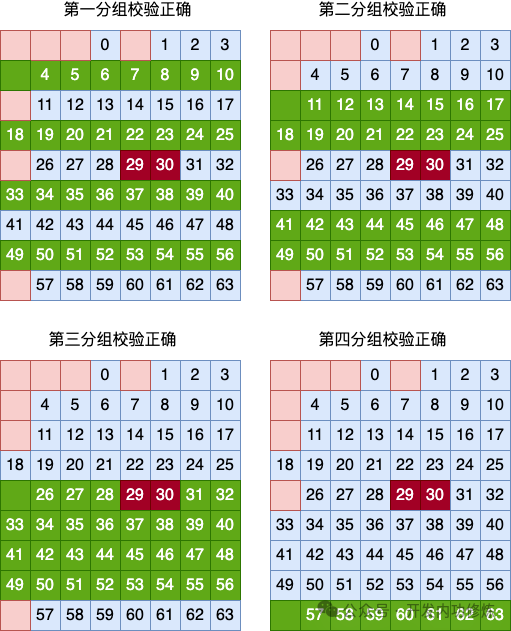 图片
图片总结
- 最近发表
- 随机阅读
- 五个容易被忽视的物理数据中心安全威胁
- 老铁,东北话编程了解一下不?谷歌工程师新作!
- 用Python执行程序的4种方式,编程必备
- 一文完全吃透JavaScript继承(面试必备良药)
- 开创可持续数据中心的未来
- 如何在6个月内学会Python?
- 如何在 Ubuntu Linux 中设置或更改时区
- Java无可匹敌的变身装备,钢铁侠客的绝密味道
- 步入AI新纪元:全新沃尔沃EX90 SUV基于NVIDIA DRIVE打造而成
- 数据分析实战:利用Python对心脏病数据集进行分析
- Android Context完全解析你所不知道的各种细节
- 10个节省时间和改善工作流的Git技巧
- 2023年数据中心的六大趋势
- 你所不知道的Python技巧|系列1
- 循序渐进 理解什么是Java内存模型
- Kubernetes部署的五项安全优秀实践
- AI热潮下,芯片制造商将芯片堆叠起来,就像搭积木
- 面试官提到的 AVL 树,到底是个啥
- 疫情期,APP 崩了怎么办?阿里工程师公开高可用架构笔记
- 惊讶!我定的日志规范被CTO在全公司推广了
- 搜索